¶ Biosensors and Bioelectronics
¶ High-resolution CMOS-based biosensor for assessing hippocampal circuit dynamics in experience-dependent plasticity
Brett Addison Emery a,1, Xin Hu a,1, Shahrukh Khanzada a, Gerd Kempermann b,c,2, Hayder Amin a,d,*,2
a Research Group “Bobrideuroelectronics”, Center for Neurodegenerative Diseases (E),atzberg 43 Dresden
b Research Group “Adult Neurogenesis”, Gean Center for Neurodegenerative Diseases (E),atzberg 43 Dresden
c Center for Regenerative Therapies TU Dresden (CRTD), Fetscherstraße 105, 01307 Dresden, Germany
d TU Dresden, Faculty of Medicine Carl Gustav Carus, Bergstraße 53, 01069 Dresden, Germany
- Corresponding author. Research Group “Biohybrid Neuroelectronics”, German Center for Neurodegenerative Diseases (DZNE), Tatzberg 41, 01307, Dresden,Germany.
E-mail address: hayder.amin@dzne.de (H. Amin).
1 shared first authorship.
2 shared senior authorship.
¶ Keywords:
Large-scale biosensors
Neural circuit
CMOS-MEAs
Connectome
Graph theory
Enriched environment
¶ ABSTRACT
Experiential richness creates tissue-level changes and synaptic plasticity as paterns emerge from rhythmic spatiotemporal activity of large interconnected neuronal asemblies.Despite numerous experimental and computational approaches at different scales,the precise impact of experience on network-wide computational dynamics remains inaccessible due to the lack of applicable large-scale recording methodology.We here demonstratea large-scale multi-site biohybrid brain circuity on-CMOs-based biosensor with an unprecedented spatiotemporal resolution of 4096 microelectrodes,which allows simultaneous electrophysiological assessment across the entire hippocampal-cortical subnetworks from mice living in an enriched environment (ENR) and standard-housed (SD)conditions.Our platform,empowered with various computational analyses,reveals environmental enrichment’s impacts on local and global spatiotemporal neural dynamics,firing synchrony, topological network complexity,and large-scale connectome.Our results delineate the distinct role of prior experience in enhancing multiplexed dimensionalcoding formed by neuronal ensembles and error tolerance and resilience to random failures compared to standard conditions.The scope and depth of these efects highlight the critical role of high-density,large-scale biosensors to provide anew understanding of the computational dynamics and information procesing in multimodal physiological and experience-dependent plasticity conditions and their role in higher brain functions.Knowledge of these large-scale dynamics can inspire the development of biologically plausible computational models and computational artificial intelligence networks and expand the reach of neuromorphic brain-inspired computing into new applications.
¶ 1.Introduction
The hippocampus plays a central role in spatial, contextual,and episodic learning. It also represents a brain region capable of undergoing structural and functional changes in response to various stimuli, thus demonstrating its plasticity (Bird and Burgess,2008; Lisman et al., 2017).This plasticity is an activity-dependent process,and it has been linked to experience-dependent changes and neurogenesis (Kempermann et al., 20l5). Over the past few decades,work has revealed much insight into individual cell types,synaptic machinery and plasticity,and action potentials in the major routes of information flow through the hippocampus (Lisman et al., 2017; Andersen et al., 2007). Nevertheless, little is known about how the individual circuit components dynamically interact to form cell assemblies (i.e.,microcircuits) in hippocampal subnetworks and how this contributes to dynamically shaping the processing of information underlying learning and memory. Specific functionality within the hippocampal circuitry has been usually identified in relation to the canonical tri-synaptic pathway to relay information from the entorhinal cortex (EC) to the dentate gyrus (DG),then processed further to CA3 and CA1 before back-projecting to the entorhinal cortex (EC) (Amaral and Witter,1989). This pathway is,however,only one possble route by which information is processed in the hippocampus, and the EC may not be the only primary extrinsic input to consider. Indeed,electrophysiological recordings in hippocampal slices demonstrated evidence of back-projections from CA3 to DG and CA3 (Scharfman, 2007). Computational modeling predicted improved pattern separation and completion and increased storage capacity in the CA3 (Myers and Scharfman, 2Ol1) due to such architecture. This pathway might also play a role in seizure activity originating in the ventral hippocampus (Scharfman, 2007).
In mammals, the DG is one of the only two brain regions (together with the olfactory bulb) in which neurogenesis continues throughout life,providing a particular type of neural plasticity (Altman and Das, 1965; Lepousez et al., 2013). In the DG,adult neurogenesis continuously generates new granule cell neurons that integrate into the tri-synaptic circuitry.They participate in the known network functions,affect computational dynamics (Kempermann, 2003; Aimone et al., 2009) and contribute to information processing,conjunctive encoding,cognition, and emotional regulation (Miller and Sahay, 2019).
Rhythmic dynamics of local field potentials (LFPs) emerge from postsynaptic currents and reflect activity in cell assemblies.These can be takenas a proxy to investigate mechanisms underlying content-specific representations during encoding and transmitting information through the hippocampal circuitry (Watrous et al., 2015). Consequently,for further progress in understanding the computational principles governing this highly plastic system,it is necessary to examine the electrophysiological features of the network architecture and the dynamics of oscillatory activity in hippocampal-cortical subnetworks at much greater depth and resolution as previously possible (Sirota and Buzsaki, 2005).To satisfy these demands,acute brain slices on-chip’represent a very powerful experimental tool for studying neurophysiological processes across scales from cellular to network levels (Huang et al., 2012). Many studies have already exploited slice-based biosensors to report experimental paradigms with spiking and LFP activity recordings from individual and network-wide electrogenic cell assembliesusing patch-clamp recordings (Reyes,2O19) and microelectrode array (MEAs) devices (Soe et al., 2Ol2).In our work,we take a significant step further to advance this area of research.
The importance and unique multi-layer dimensionality of the hippocampal circuitry,additionally empowered byneurogenesisdependent plasticity,has triggered the development of several braininspired computational models of intelligence and learning paradigms and has inspired novel approaches in neuromorphic computing (Schuman et al., 2022; Wu et al., 2022; Aimone and Gage, 2011; Zhang et al., 2020).They also indicate novel lifelong learning approaches (Kudithipudi et al.,2022) and might even promise advances in biomimetic prosthetic devices for restoring and enhancing memory functions impaired in diseases and injuries (Hampson et al.,2O18).Despite these perspectives,actual further advancements in new learning algorithms for developing scalable on-chip biological-based computing networks have been challenged by the as-yet limited understanding of the hippocampal connectome (Frenkel, 2O21) arising from the interaction of dynamical neuronal ensembles.As we show here,large-scale recording methods that enable the simultaneous recordings of extracellular rhythmic activity with a single device allow us to effectively address this challenge (Emery et al., 2022; Buzsaki et al., 2015; Hu et al., 2022; Jun et al., 2017).
In this study,we developed a neuroelectronics-based platform specifically focusing on how large-scale oscillatory dynamics of communication and the flow of information in hippocampal-cortical subnetworks are shaped by prior experience.While the classical experimental paradigm of environmental enrichment (ENR) has led to a large body of evidence about how environmental stimuli affect the brain, including the promotion of adult neurogenesis in the dentate gyrus (Kempermann, 2019; Mohammed et al., 2002; Nithianantharajah and Hannan, 2006), knowledge about ENR-induced large-scale effects on hippocampal circuits and their activity has been very scarce (Tuncdemir et al., 2019). These effects have been generally implicated in the notion that the brain’s fine structure depends on past activity in the network(Tuncdemir et al.,2O19).The historical unavailability of large-scale neural recording methodologies partly explains the as-yet inadequate evidence. Large-scale electrophysiology has been inaccessible,and while non-invasive MRI in humans suggests that enrichment has global network effects (Urban-Wojcik et al., 2021),it does not have a sufficient spatiotemporal resolution to investigate the microscale network organization and information processing in rodents (Little et al.,2012; Manno et al.,2022). The computational dynamics and connectome of large-scale hippocampal networks and their modification by experience have thus largely remained elusive.Electrophysiological studies comparing hippocampal circuits of rodents housed in an enriched environment (ENR) with standard-housed animals (SD) revealed enrichment-dependent effects on long-term potentiation (LTP) in idividual neurons (Ohline and Abraham, 2019),and gamma oscillation enhancement in CAl (Shinohara et al., 2Ol3), but with the low number of recorded cells could not generalize to the hippocampal network-wide connectome.Further studies also revealed the basic local connectivity of adult-born neurons (Christian et al., 2014; Restivo et al., 2015) and experience-dependent structural synaptic plasticity (Holtmaat and Svoboda, 2Oo9).At the same time,rabies virus-based tracing was used to identify the remodeling of structural connectivity by ENR (Bergami et al.,2Ol5).However,all these previous reports could not answer the fundamental question of if and how ENR could promote the refinement and rewiring of the connectome.As simultaneous recordings of circuit-wide activity are required to estimate the large-scale wiring diagrams of neural circuitry and determine the input/output transformation directly under experience,we hypothesize that previous studies might have qualitatively and quantitativelyunderestimated the change that rich experience brings to the large-scale hippocampal circuitry and its functions.
Recent advancements in active-pixel biosensors (Berdondini et al., 2005;Imfeld et al., 2008) through thecomplementary metal-oxide-semiconductor (CMOs) technology have been exploited in many applications in neurosciences and biomedical engineering (Emery et al., 2022; Hu et al., 2022; Amin et al., 2017). In vitro (Amin, 2016) and in vivo (Angotzi et al.,2Ol9) measurements of bioelectrical signals that can be simultaneously obtained from thousands of electrodes at high spatiotemporal resolution have become possible by the distinctive features of these devices,including on-chip addressing,multiplexing,and high signal-to-noise ratios (Imfeld et al., 2008). Although high-density biosensors have laid the foundation for studying network-wide hippocampal-cortical epileptiform activity (Ferrea et al., 2Ol2),understanding the large-scale computational dynamics of hippocampal-cortical circuitry under physiological conditions has dramatically lagged behind.
We here report a novel,non-invasive,multi-site,long-term,and label-free large-scale brain-chip-based biosensor implemented in a CMOS-high-density microelectrode array (Hu et al., 2022; Imfeld et al., 2008) (HD-neurochip) with integrative advanced computational analyses.The array size over with 4096 microelectrodes enabled simultaneous measuring and mapped multidimensional neural information dynamics across the entire rodent hippocampal-cortical circuit obtained from ENR and SD mice. Our results provide an unprecedented mesoscopic large-scale quantification of the circuit-wide functional connectivity and reveal the distinct effects of prior experience on spatiotemporal network dynamics and encoding information. Knowledge of these large-scale dynamics in the hippocampus may enable more efficient neuroscience-oriented computational models,promote the development of next-generation artificial intelligence networks,and expand the reach of memory neuromorphic brain-inspired sensors and chips into new applications in health and disease.
¶ 2.Materials and methods
¶ Animals and housing conditions.
All experiments were performed on 12-week-old C57BL/6J mice in accordance with the applicable European and national regulations (Tierschutzgesetz) and were approved by the local authority (Landesdirektion Sachsen; 25-5131/476/14). Female C57BL/6Jmice were obtained from (Charles River Laboratories, Germany) at five weeks of age and randomly distributed at six weeks of age into two experimental groups - standard (SD) housed and enriched environment (ENR) housed as previously reported (Garthe etal., 2016). Briefly,mice were placed in standard mouse cages (at least 4 per cage) with nesting materials and food and water ad libitum. Another group of mice (at least 8 per cage) was placed in larger cages allowing more differentiated social interactions compared to SD.ENR mice lived in specially designed larger cages equipped with rearrangeable toys,maze-like plastic tubes, tunnels with various openings, houses,additional nesting material,and food and water ad libitum. Food type and nesting material were standardized between the two experimental groups.Nesting material was changed weekly,with ENR cages receiving rearrangement of all additional structures providing learning opportunities.This allows the ENR cage environment to provide stimuli as well as differentiated social interactions.Mice stayed in the assigned environment for six weeks before the experiments began and remained until their experimental date.Mice were randomly selected between both groups on each experimental day,with a batch of recording experiments lasting one week.
¶ Acute brain slice preparation.
Mice were anesthetized with isoflurane before decapitation. Brain slices were prepared according to our previous study (Hu et al., 2022). Briefly, the brain was carefully removed from the skull and placed in a chilled cutting sucrose solution before slicing. The brain was securely placed inside a custom-made agarose-based container, which was then fixed onto the cutting plate. Dorsal horizontal slices (300 μm thick) were prepared from both brain hemispheres using Leica Vibratome VT1200S (Leica Microsystems, Germany). Slices were cut at 0–2 °C in aCSF solution saturated with 95% O₂ and 5% CO₂ (pH = 7.2–7.4) of a high sucrose solution containing (in mM):250 Sucrose, 10 Glucose, 1.25 NaH₂PO₄, 24 NaHCO₃, 2.5 KCl, 0.5 Ascorbic acid, 4 MgCl₂, 1.2 MgSO₄, 0.5 CaCl₂. Next, hippocampal-cortical slices were incubated for 45 min at 34 °C and then recovered at room temperature for at least 1 h before recordings with a high-density neurochip. Perfusate used during recordings contained (in mM):127 NaCl, 2.5 KCl, 1.25 NaH₂PO₄, 24 NaHCO₃, 25 Glucose, 1.25 MgSO₄, 2 CaCl₂,and was aerated with 95% O₂ and 5% CO₂.
¶ Large-scale CMOs-based biosensor recordings.
Extracellular recordings were performed using high-density (HD) CMOs chips incorporated into an acquisition system (3Brain AG,Switzerland) customized to our recording setup.HD neurochips are composed of 4096 recording electrodes with a pitch size to contain an active sensing area of ,ideal for recording entire hippocampal-parahippocampal cortical regions.The on-chip amplification circuit allows for 0.1-5 kHz band-pass filtering conferred by a global gain of sufficient to record slow and fast oscillations (Hu et al.,2O22).High-density platinum-black (Pt-B) electrodes were coated with PDLO (Sigma-Aldrich,Germany)and incubated for at before recordings. Slices were moved and coupled onto the neurochips using a custom-made platinum harp placed above the tissue.A steady perfusion system was built to deliver oxygenated recording perfusate to the slice-neurochip interface with a flow rate of and was temperature controlled at throughout the experiment and recordings. We acquired extracellular recordings at /electrode sampling frequency from spontaneous activity through pharmacologically-evoked responses using 4-aminopyridine (4-AP) (Sigma-Aldrich,Germany).A modular Stereomicroscope (Leica Microsystems,Germany) was designed and incorporated into the setup to capture the acute slices light-imaging simultaneously with the whole-circuit extracellular recordings.These images were further used to obtain the spatial organization of tissue relative to the firing electrode layout during analysis.Events of LFPs and multi-unit activity (MUA) activity were detected with hard threshold and precise timing spike detection algorithms (PTsD) (Maccione et al., 2009) algorithms and were performed with commercially available software (3Brain AG, Switzerland). Detected events were further processed and filtered with a low-pass filter for LFPs,a band-pass filter for MUAs, and a band-pass filter for ripple-like events.Additionally, LFP waveforms were band-pass filtered using a 4th-order Butterworth filter at delta ,theta (5-12),beta (13-35),and gamma (35-100) bands.
¶ Data analysis.
All basic and advanced algorithms used in this work were developed and implemented with custom-written Python scripts. Any package add-ons are cited accordingly.
¶ Structural clusters.
To characterize hippocampal-cortical subnetworks behavior locally and globally,the functional firing electrodes were structurally related to a specific slice region.Thus,light microscope hippocampal images were overlayed on the neurochip microelectrodes layout (i.e.,functional-structural overlay).Electrodes were thengrouped based on annotated structural markers on the hippocampal-cortical slice.These clusters included six major regions of the hippocampal-parahippocampal cortical circuitry -DG,Hilus,CA1, CA3,EC,and PC.
¶ Mean activity basic analysis.
We selected three parameters to describe the mean activity features of large-scale spatiotemporal LFP oscillations, including LFP rate, amplitude, and event delay. LFP rate was defined as the number of detected LFP events per minute, and the event delay was defined as the time interval between consecutive detected events. The signal amplitude was obtained through full-wave rectification and low-pass filtering with a cut-off frequency of 100 Hz.
¶ Ripple event detection and analysis.
We employed a multi-site averaging method (Kay et al., 2016) to detect ripple events in the hippocampal network. The raw LFP signals recorded from multiple spatial locations were bandpass-filtered between 140 and 220 Hz. Subsequently, the event envelope was ascertained through a Hilbert transform and smoothed using a Gaussian function with a 4 ms standard deviation (SD). Spatiotemporal events were identified when the smoothed envelope exceeded 3 SD above the mean for a minimum duration of 15 ms. The frequency of occurrence and amplitude of ripples were then calculated based on the average of all detected events.
¶ Time-frequency and power spectrum density (PsD) analyses.
To determine the power distribution of the LFPs and the dominant frequencies within an oscillatory event, we constructed frequency-time dynamics in pseudo-color spectrograms for a selected time window using filtered LFPs (1–100 Hz). To estimate the power spectral density (PSD), we used Welch’s method, as previously described (Hu et al., 2022), by calculating the Fast Fourier Transform (FFT) of the detected LFPs.
¶ Lognormal distribution.
The LFP firing patterns of the hippocampal neuronal ensembles showed a wide degree of participation in the circuit activity and followed a skewed lognormal distribution.Thus,we computed the probability density function for the lognormal distribution as previously described (Hu et al., 2022).
Where is the mean, and is the standard deviation.
¶ Gini coefficient.
To quantify the inequality of participation of individual ensembles in the interconnected layers of the hippocampal circuit,we employed the Gini index,which was computed as the ratio of the areas on the Lorenz curve diagram (Hu et al., 2022).
Where is the area above the Lorenz curve,and is the area below the cumulative LFP firing rates.
¶ Spatiotemporal LFP trajectories.
To quantify the propagation magnitude of the spatiotemporal LFP events in all interconnected hippocampal layers,we employed the center-of-activity trajectories (CATs) analysis (Hu et al.,2022).Voltage values embedded in the LFP frame activities within a 5 ms moving time bin were used to collect the CAT magnitudes in each firing event.The value of the CAT at time isa two-dimensional vector.
Where denotes the LFP firing rate corresponding to the active electrodes within a time window ™. and are the column and row numbers of the associated E. and are the coordinates of the physical center of electrodes. is the total number of active electrodes.Then, the CA trajectory from to with a time step can be computed.
Based on the spatiotemporal trajectories for all the firing events, we categorized the propagation pathways of firing events in the interconnected hippocampal-cortical network into three major groups:i) From the hippocampus to entorhinal/perirhinal cortical regions (Hippocampus → EC/PC);ii) From entorhinal cortex to hippocampus (EC → Hippocampus);iii) Intra-hippocampal circuits (only hippocampus).
¶ CATs-based velocity.
To track and map the putative rate of spatiotemporal displacement of LFP events over the entire hippocampalcortical interconnected layers with minimum reliance on slice structure and labeling methods,we calculated the velocity of the reconstructed CATs.We computed the distance from the beginning to the end of instantaneous vector quantity displacements of averaged CATs across layers using the known physical dimensions of electrode coordinates and size.Subsequently,we divided these displacements by the total time of associated firing events throughout the recording duration (Hu et al., 2022).
Where is the change in displacement, and is the change in time.
¶ LFP-spike information analysis.
To quantify the information carried by phases of individual LFP fluctuations at the time of multi-unit spiking activity,we employed a four-step procedure;i)we extracted individual frequency information from a multi-layered hippocampalcortical network at band,resulting from our power frequency analysis; ii) we computed the instantaneous phase values (i.e.,with precision,where the phase values and correspond to the peak and trough of the oscillation,respectively) of the narrow-band waveform fluctuations in multiple events using the Hilbert transform.This allowed us to visualize the LFP phases in color-coded equispaced quadrants; iii) we extracted multi-unit spiking activity (MUA) from the interconnected hippocampal layers using the precise timing spike detection algorithm (Maccione et al.,2Oo9) with a threshold set to 8 standard deviations of the band-pass filtered signal (Butterworth filter,4th order) at ).We then labeled the spikes with the color of the LFP phase quadrants at the time of their occurrence and presented them in rastergrams and rate code plots; iv) next,we quantified the information carried by the phase of the LFPs and characterized in units of bits using the information-theoretic analysis (Mazzoni et al., 2013).
¶ Functional connectivity and causality.
Cross-covariance was calculated between pairs of electrodes in the arrayusing Pearson’s correlation coefficient (PCC) to infer large-scale statistically dependent connectivity ona multi-layered hippocampal network.This was followed by performing Multivariate Granger causality to quantify the influence of one time series on another and Directed Transfer Function (DTF) to measure directional information flow as we previously described (Hu et al., 2O22).All the electrodes were sorted by hippocampal-cortical subnetwork clusters,and the statistic calculations for PCC and interconnection links count were based on paired clusters.
¶ Network connectivity metrics.
Graph Theory was used to characterize overall network topology and interconnectedness from detected LFP events.We computed the graph metrics in custom-written Python code and adapted functions from NetworkX-python package (Hagberg et al.,2008),available on GitHub (https://github.com/networkx). Briefly,the functional network connectivity metrics are described by considering node as the central component of the graph that may or may not be connected to one another.In our case,a node corresponds to a specific electrode in the sensing array.Also,the edges e are the functional links or connections between each node
¶ Degree.
To characterize the different representations of network connectivity,we characterized the degree of a node to describe the number of edges connected to a node.We also computed the in-degree or out-degree based on the direction of the vectors (i.e.,the flow of information).
Where denotes the degree of a node i. denotes the connection between nodes i and j. is the set of all computed nodes in the network, is in-degree and out-degree of node respectively.
¶ Degree centrality.
To determine nodes with high topological centrality and influence on network function,the centrality was computed as the normalized fraction of nodes that node i connected to (Rubinov and Sporns, 2010).
¶ Clustering coefficient.
To measure how nodes in a given network tend to cluster together to assess the functional segregation, the clustering coefficient (CCi) was computed (Rubinov and Sporns, 2010).
Where denotes the number neighbors to node and denotes the number of links connecting the to the node i.
Transitivity.To reveal the existence of tightly connected communities,transitivity was characterized as the fraction of all possble connected triangles to describe two edges with a shared vertex in a network (Rubinov and Sporns, 2010).
Where is the actual number of triangles in a network and is the number of triads or possible triangles that consist of two edges with a shared vertex.
¶ Average shortest path length.
To measure the functional integration of the information flow between layers in the network,the average shortest path length was computed (Rubinov and Sporns, 2010).
Where denotes the shortest path from i to and is normalized over all possible paired numbers of nodes in the network.
¶ Hub nodes and rich club nodes.
To determine centralized,essential nodes in a network and reveal network topology,hub nodes and rich club nodes were analyzed.Hub nodes were detected based on three nodal metrics - node strength,clustering coefficient,and network efficiency.The metric value for each node was calculated and compared to determine whether the node value was in the top of all nodes (Schroeter et al.,2O15).To restrict the definition of the hub node, we set limits with a hub score.Our hub score was valued between O and 3, where nodes either satisfied the top in none,1,2,or all 3 nodal metrics.Within the hub node group is a subgroup of nodes with dense connections that conferred the rich-club nodes and are described as hub nodes with a higher degree than the average and provided by the rich club coefficient (Kim and Min, 2020).
Where denotes the degree, represents the number of nodes whose degree is larger than a given value and denotes the number of connections in a subnetwork comprising n _
¶ Network topology characterization.
To determine the potential impact of hub nodes on the network function and the organizational processes shaping network topology,we characterized the degree distributions of detected nodes in SD and ENR datasets,which resulted in decayed distribution with a power-low tail (Barabasi and Albert, 1999).
To estimate the power-low degree distribution to describe the scale-free topology with small-world attributes,we used the lognormal model fit.
Where and are the mean and standard deviation of the distribution, respectively.
To visualize the best-fit network characterization,a complementary cumulative distribution function (cCDF) was used instead of the probability density of the node degree and plotted on logarithmic axes for a more robust visualization of the high regime.Goodness-of-fit tests were performed between actual data and fitted models and were estimated by the coefficient of determination R ^
¶ Robustness.
To estimate the robustness and flexibility of networks for error tolerance and attack vulnerability, we employed two strategies; i) for error tolerance,we measured the node degree and remaining links aftera fraction of nodes were randomly removed; ii) for attack vulnerability,we measured the remaining links in the network after stepwise removal of high degree nodes.
Graph map visualization.To visualize the large-scale network connectivity maps,we constructed the data architecture containing nodes and edges.This setup allowed marking the node IDs,coordinates, labels,edge sources,and edge targets.These maps were then converted into(.gexf) file format and were directly read and visualized in the Gephi program 9.2 version (https://gephi.org).To compare the ENR v. SD,the top of the total functional links were plotted with similar edge weights and degree range queries.
¶ Dimensionality.
To characterize the link between network-wide collective activity and connectivity,we computed network dimensionality (Litwin-Kumar et al., 2Ol7).The functional connections or links between paired electrodes across all LFP events in a recording time window served as an input.The dimensionality is defined as the weighted measure of the number of axes of all firing electrodes in the activity population space.
Where is the eigenvalue of covariance matrix X. The resulting value was normalized over the maximum dimensionality value to give a data
range from 0 to 1.
¶ Statistical analysis.
All statistical analyses were performed with Originlab 2020.All data in this work were expressed as the mean standard error of the mean (SEM).All box charts are determined by the 25th-75th percentiles and the whiskers by the 5th- 95th percentiles and lengths within the Interquartile range (1.5 IQR).Also,the lines depict the median and the squares for the mean values.Differences between groups were examined for statistical significance,where appropriate, using the Kolmogorov-Smirnov test,Mann-Whitney test,one-way analysis of variance (ANOVA),or two-way ANOVA followed by Tukey’s posthoc testing. was considered significant.Detailed statistical results are provided in .Supplementary Tables 1 and 2
¶ 3.Results and discussion
¶ 3.1.High spatiotemporal resolution biosensing platform
To begin,we implemented a large-scale multi-site CMOS-based biosensing platform with an integrative computational framework, which allowed us to probe the dynamical impact of experience-induced functional complexity in the hippocampal-parahippocampal cortical (i. e., hippocampal-cortical) circuitry. Acute brain slices from mice reared in enriched environmental conditions (ENR) compared to standard housing (SD) were coupled to a high-density CMOS-based chip (i.e., 4096 electrodes with a pitch size) (Hu et al., 2022; Imfeld et al., 2008) to allow recording a rich repertoire of spontaneous activity generated through pharmacologically-evoked sub-milisecond extracellular firing information sampled simultaneously from the entire hippocampal-cortical circuitry(Fig. la-c). Weoutlinedthe hippocampal-cortical circuit as six interconnected regions (DG,Hilus, CA3,CA1,entorhinal cortex ‘EC’,and perirhinal cortex ‘PC’) by overlaying the bioelectrical functional readouts on the corresponding anatomical subregions. This information was acquired concurrently with optical imaging. Our Brain-Chip biosensor readouts provided real-time firing activity sampled spatially from single pixel-like sensors (i.e., pixel-array) in the format of sequential bioelectrical frames. On large-scale subnetworks,each sensing pixel’s encoded extracellular voltage signals were visualized with a false-color mapping,illustrating real-time bioimaging video frames of the entire hippocampal-cortical functional circuit (Fig.lc).To improve the communication between the whole hippocampal-cortical slice and the high-density biosensing chip,leading to high-quality signal recordings with an enhanced signal-to-noise ratio,we biofunctionalized the porous platinum-black (Pt-B) coated electrodes using the adhesion-promoting molecule, poly-DL-ornithine (PDLO). The combination of Pt-B’s electrochemical properties (Abbott et al., 202O) and the PDLO molecule (Amin et al., 2018) increased surface area for electrical signal detection and better electrical conductivity, ultimately improving tissue-electrode coupling. This optimized coupling significantly contributed to our platform’s overall performance,allowing for precise and reliable analysis of the network-wide mesoscale ex vivo connectome and spatiotemporal firing patterns influenced by ENR,as demonstrated in the subsequent sections. We also implemented a novel computational framework for multidimensional datasets to extract unique dynamical features (i.e., firing initiation and propagation, frequency spectrum properties, spike-LFP dynamics,functional connectivity,and network-wide topology) in order to uncover individual neural computations implicated in large-scale activity dynamics under experience-dependent enhancement (Fig.ld-f). With this,our next-generation experimental-computational platform was designed to target the fundamental question of how exposure to ENR remodels the architecture, topology, and coding dynamics of concrete functional neuronal networks,as these would explain the well-described enhancement of cognitive capabilities in ENR (Lisman et al., 2017).
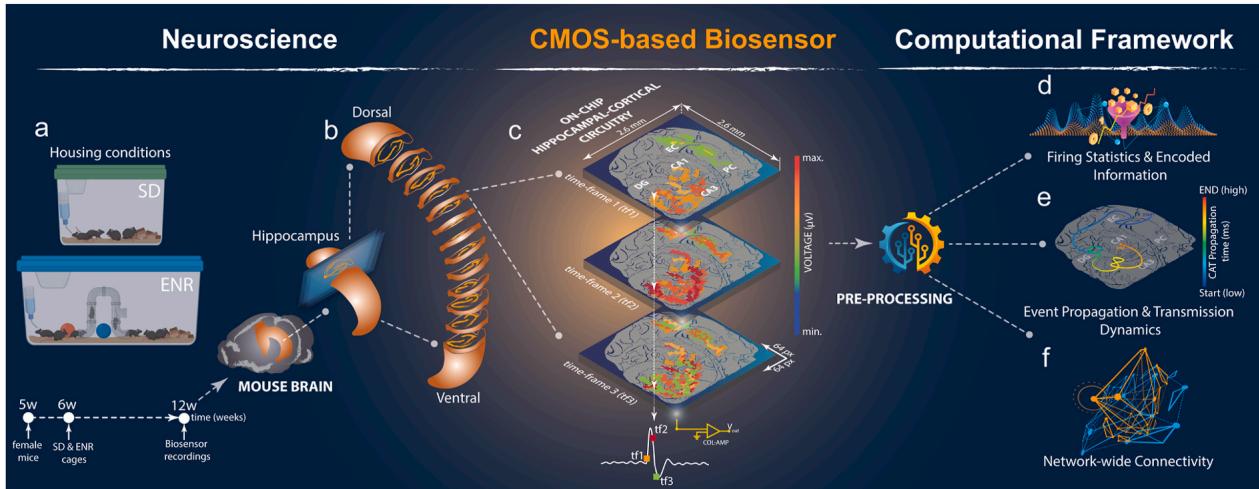
Fig. 1. Large-scale CMOS-based Biosensor Framework. a) Schematic representation of mouse living conditions in SD and ENR experimental groups and the timeline. ENR cage introduces novel objects, exploration, and social interactions compared to SD. b) Graphical illustration of mouse brain depicting the hippocampal region isolated and sectioned horizontally to be interfaced with the CMOS chip. c) Isometric imaging setup featuring the hippocampal-cortical slice coupled to aCMOS-chip with 64 x 64 electrode array identified by Pixel-multi-frame real-time representation of the encoded network-wide activity enabling pseudo-color reconstruction of the entire circuit firing information from sequential frames. d-f) Integrative computational pipeline customized to preprocess multidimensional readouts obtained from multi-layered Hippocampal-cortical subnetworks to provide first-order statistical analysis, dynamical assessment, functional network connectivity, and topological complexity characterization.
¶ 3.2.Spatiotemporal network-wide firing activity and dynamics
To address the significance of using a large-scale acute brain slicebased biosensor to unveil the impact of ENR on recurring transient neural activity,we recorded spontaneous network-wide activity through pharmacologically-evoked responses (i.e.,applying 4-aminopyridine ‘4- AP’).We computed and quantified the first-order statistical parameters of the spatiotemporal population firing patterns that demonstrated substantial responses in the ENR subnetworks,indicated by higher LFP rates,signal amplitude,and shorter delay features between consecutive LFP events (Fig. 2a-d and Supplementary movies 1-2). The oscillatory activity pattern of neural ensembles between hippocampal and cortical networks is essential for learning and memory,connecting synaptic plasticity and network information processing (Buzsaki,1989; Lisman et al., 2Oo5).We detected rhythmic firing initiating in CA3 and propagating to other hippocampal-cortical subnetworks that emerged from slow oscillation (below superimposed by faster fluctuations (up to ${ 2 0 0 } \ \mathrm { H z } $ .Compared to SD,ENRnetworksyielded patternsofhigher synchronicity (Fig.2e and i) associated with increased superimposed ripple-like patterns in the hippocampal network,indicated by significantly higher frequency,inter-ripple-intervals (IRIs),and amplitude in ENR than SD (Fig. 2f-h and j-l, and Supplementary Fig.1). These features endowed the active neuronal ensembles in ENR networks with more rhythm generators (Buzsaki, 2Oo2) and more functionally connected anatomical subnetworks (McCormick and Contreras,2001). These results may suggest a mechanism by which ENR improves the encoding and flow of spatiotemporal information (Shinohara et al., 2013; Colgin et al., 2009).
It has been shown in different brain regions that collective functional features of neuronal networks emerge from multiplicative and synergistic interactive parameters (i.e.,firing patterns of synchronized neuronal populations),giving rise to skewed lognormal distributions, which permeate every level of brain organization. These networks with pre-configured skewed distributions conferred broad dynamical properties,facilitating stability,resilience,and tolerance to failure (Hu et al., 2022; Buzsaki and Mizuseki, 2014).
Therefore,we assessed the firing rate distributions in ENR and SD recordings.We found that in ENR,the neuronal participation in synchronous network events showed strongly skewed lognormal distributions.A small fraction of firing electrodes generated a higher firing frequency than SD (Fig. 2m and n,and Supplementary Fig. 2). In ENR networks,the asymmetric variation of firing distributions in different hippocampal-cortical subregions showed a significant extension of the right tail toward higher frequencies (DG, ,Hilus, CA1, ,CA3, ,EC, $p < 1 0 ^ { - 9 3 } $ mogorov-Smirnov test).To further quantify the inequality in the contribution of population synchrony and information content of firing electrodes across the entire network,we computed the Gini index from the Lorenz curve (Hurley and Rickard, 20o9) (Fig. 2m and n insets) - the higher the index,the more unequal the participation of the firing electrodes.Intriguingly,we observed higher Gini coefficients in SD firing populations (higher inequality with most electrodes firing at a low rate) than in the ENR network,with many more electrodes contributing to recorded events (Fig.3o).These results suggest that in ENR,the interconnected hippocampal subnetworks of highly firing neuronal ensembles support collective stability and flexibility for continuous network remodeling without affecting global stability (Panas et al., 2015).
Together,our results identified large-scale functional implications of enhanced oscillatory patterns in the ENR hippocampal-cortical subnetworks. The increased excitability and synchronous dynamics observed in ENR may suggest an enhanced involvement in rhythm generation (Buzsaki, 2Oo2) and improved network stability (Butler and Paulsen, 2015; Jercog et al., 2017). However, further investigation is required to establish these relationships.
¶ 3.3.Mapping information flow and firing patens complexity
The hippocampal circuit propagates information primarily through chemical synaptic transmission mediated in two pathways - serially along the tri-synaptic transmission from EC to DG, then to CA3 and CA1 (Amaral and Witter, 1989),and via recurrent di-synaptic networks between CA3 and DG (Scharfman, 2Oo7).Additionally, high-frequency oscillations could be propagated via gap junctions (Draguhn et al., 1998), while the propagation of slow oscillatory activity is modulated by non-synaptic ephaptic coupling (Frohlich and McCormick, 201O).We used the simultaneous large-scale recordings from all subnetworks to quantify the long-range propagation incidence of 4-AP-induced firing oscillations.In region CA3 of ENR hippocampi, we found more localized firing activity ignition sites than in SD (Fig.3a and b).The restricted activity distribution in CA3 propagated broadly towards adjacent and distal areas of CAl and via the recurrent network pathway back to the hilus and DG.Also,the activity incidence probability was significantly higher in all subregions after ENR (Fig.3c).We calculated the time lag between consecutive events in each subregion and found that the probability of firing and coordination level (synchrony) were higher in ENR (Fig. 3d and insets).
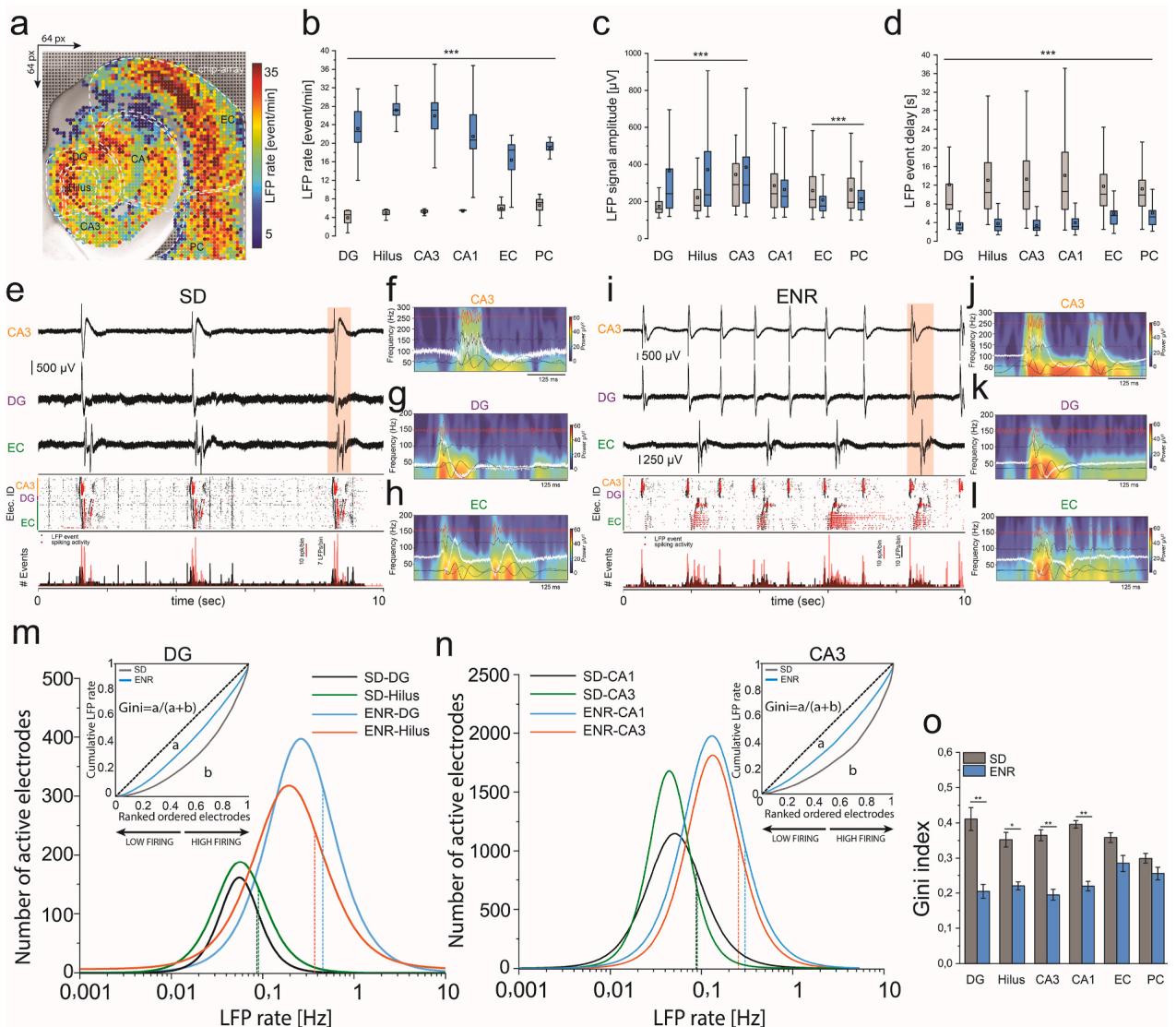
Fig. 2. Large-scale Spatiotemporal Firing Features and Network Synchrony.a) Topographical pseudo-color mapping of ENR large-scale LFP firing pattern overlaid on the hippocampal-cortical structure.b-d) Statistical quantification of the spatiotemporal firing patterns recorded simultaneously from SD vs. ENR networks illustrates significantly higher LFP rates, amplitude, and faster LFP events (i.e., shorter delay) in ENR compared to SD networks (***p < 0.001, one-way ANOVA) (n = 48 slices from 6 mice in each of the SD and ENR groups).e) Representative traces of firing waveforms aligned with the rastergram, and event counts of selected layers of CA3, DG, and EC in the SD network. The rastergram and event counts display the interconnected subnetwork with synchronous events (LFPs: black; spikes: red dots).f-h) Pseudo-color spectrograms showing the frequency-time dynamics in CA3, DG, and EC firing clusters (red-highlighted in e), respectively, overlaid with band-pass filtered waveforms to identify the firing spectrum from theta to ripple-like oscillations in SD.i) Same as (e), but for ENR, with higher synchronous and frequent events.j-l) Similar to (f–h), but for ENR firing clusters (red-highlighted in i) that show a greater magnitude of slow oscillations and ripple-like activity than SD.m-n) Firing rate distributions in different hippocampal subregions are skewed in both SD and ENR networks and conform to a lognormal distribution. The distribution in ENR depicts the activation of a substantial fraction of cells with higher firing rates than those in SD, contributing significantly to enhanced neuronal interactions. Dashed lines indicate medians (DG: p < 10⁻¹⁰⁰; Hilus: p < 10⁻¹³⁷; CA3: p < 10⁻¹⁴; CA1: p < 10⁻²¹, Kolmogorov-Smirnov test). Lorenz statistics (insets) illustrate neuronal participation in different hippocampal subnetworks (i.e., DG and CA3).o) Gini coefficients in different hippocampal-cortical regions in SD and ENR networks (*p < 0.05, **p < 0.01, one-way ANOVA). Next, we classified the center of activity trajectories (CATs) (Hu et al., 2022) with an unsupervised machine learning algorithm. We identified three propagation pathways:i) Hippocampus to EC/PC;ii) EC to hippocampus (corresponding to the classical unidirectional trisynaptic pathway);iii) Intra-hippocampal circuits mediated by the recurrent network (Fig. 3e-l). There was a more prominent propagation probability from the hippocampus to the cortex in ENR (63.2% ± 6.7%) than in SD (22.7% ± 3.3%). Although the other propagation categories were less represented in absolute terms, ENR still showed a 9-fold increase in EC-to-hippocampus propagation and a 3.5-fold increase in intra-hippocampal circuits (Fig. 3m). We then employed the reconstructed CATs for all events to calculate the rate of spatiotemporal displacement of network-wide firing events within these propagation pathways. ENR showed significantly greater mean CAT velocities (138 ± 3.3 mm/s vs. 78.1 ± 2.3 mm/s, hippocampus → EC/PC; 147 ± 10 mm/s vs. 105 ± 14.3 mm/s, EC → Hippocampus; Fig. 3n). We also found significantly shorter CAT duration in all categories after ENR (Fig. 3o).
Next, we classified the center of activity trajectories (CATs) (Huet al., 2022) with an unsupervised machine learning algorithm. We identified three propagation pathways: i) hippocampus to EC-PC, ii) EC to hippocampus, corresponding to the classical unidirectional tri-synaptic pathway, and iii) intra-hippocampal circuits mediated by the recurrent network (Fig. 3e–l). There was a more prominent propagation probability from the hippocampus to the cortex in ENR (63.2% ±
6.7) than in SD (22.7% ± 3.3). Although in absolute terms, the other propagation categories were less represented, in relative terms, ENR still showed a 9-fold increase in EC to hippocampus propagation and a 3.5-fold increase in intra-hippocampal circuits (Fig. 3m). We then employed the reconstructed CATs for all events to calculate the rate of spatiotemporal displacement of network-wide firing events within these propagation pathways. ENR showed significantly greater mean CAT
velocities (138 ± 3.3 mm/s vs. 78.1 ± 2.3 mm/s, hippocampus → EC,and 147 ± 10 mm/s vs. 105 ± 14.3 mm/s, EC → hippocampus; Fig. 3n).We also found significantly shorter CAT duration in all categories after ENR (Fig. 3o).
In conclusion, these findings demonstrated the impact of rich experience on modulating the characteristics of large-scale neural activity propagation resulting in faster information processing in the ENR than in the SD networks.This enhancement could be mediated by the feedback loop from CA3 to DG,whose sharpened network synchrony is relevant for storing and retrieving information sequences (Lisman, 1999) and facilitating pattern separation and completion (Myers and Scharfman, 2O11). The propagation features in ENR networks might be associated with increasing the tightly layered organization of the hippocampus,thereby enabling stronger endogenous local fields to induce a significant effect on neural synchronization (Francis et al., 2003).
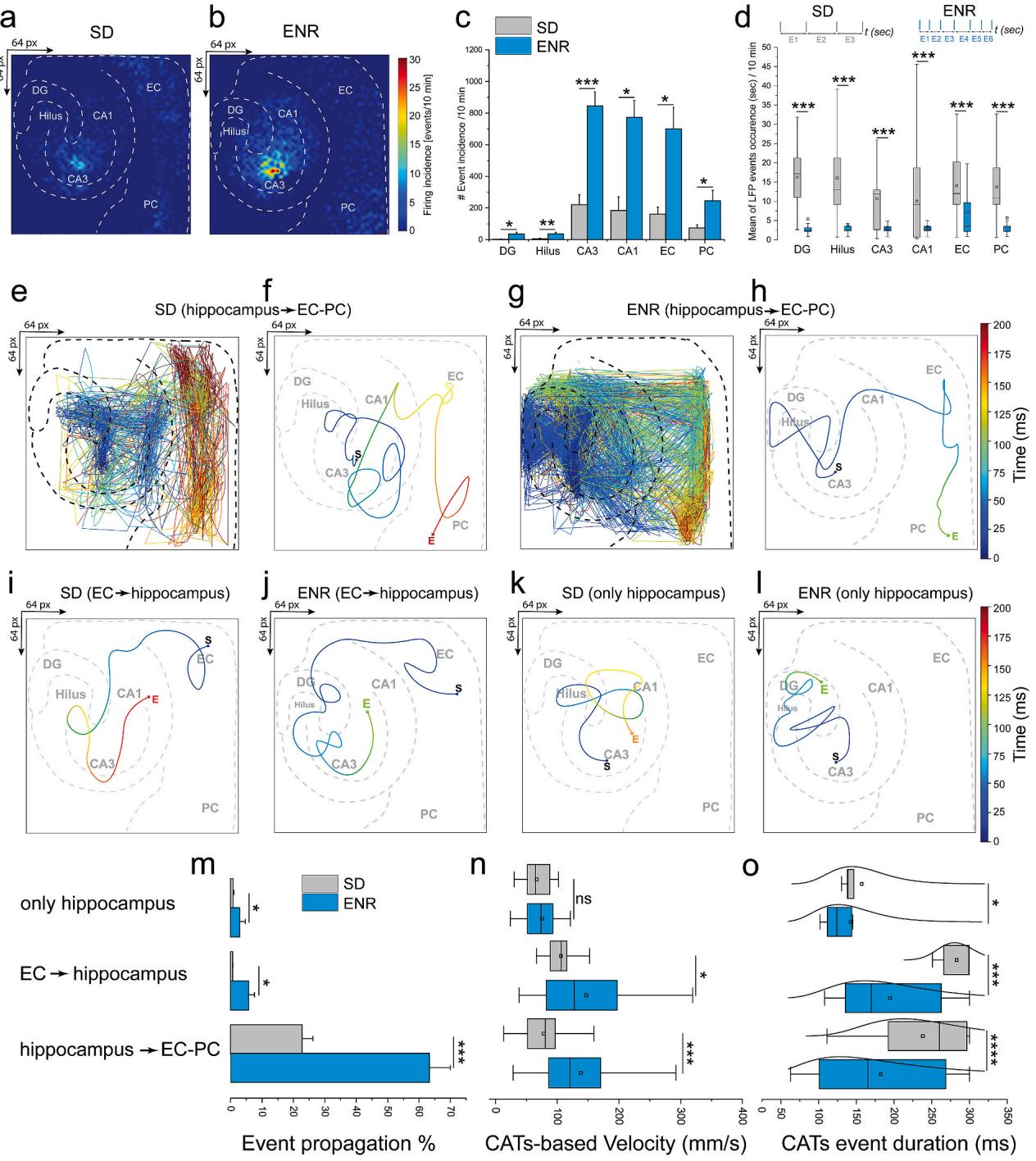
Fig. 3. Dynamical Propagation and Firing Pattern Transmission. a-b) Incidence analysis of large-scale oscillatory activity patterns. A color scale indicating event probability is computed in 10 min recordings in SD and ENR networks. Both maps show defined initiation points in the CA3 and dynamic event propagation in the hippo-cortical circuitry. c) Quantification of event incidence shows significantly higher occurrence in ENR hippo-cortical subregions than in SD. (*p < 0.05, ***p <0.001, ANOVA, n = 48 slices from 6 mice of SD and ENR each). d) Quantifying event synchrony by event delay indicating a shorter mean duration of activity events in all hippocampal-cortical subnetworks in ENR compared to SD (***p < 0.001, ANOVA, n = 48 slices from 6 mice of SD and ENR each). The time interval between successive events (insets) in SD and ENR demonstrates an example of multiple events (E) occurring with shorter delays in ENR compared to SD. e-f) Exemplary 2D CATs superimposed onto the hippocampal-cortical structural network with a color-coded time scale revealing the propagation patterns in the SD network from hippocampus→EC-PC. (e) indicating all detected activity events, and (f) showing the average event marked with starting and end spatiotemporal points. g-h) Same as in e & f but for ENR network. i-l) Same as in (f & h) but for propagation patterns from EC→hippocampus and only hippocampus in SD and ENR networks. m) Quantification of the probability of propagation events based on the classified propagation categories (i.e., hippocampus→EC-PC, EC→hippocampus, and only hippocampus). (*p < 0.05, ***p < 0.001, ANOVA, n = 48 slices from 6 mice of SD and ENR each). n) Reconstructed CATs-based velocities from inter-layer firing events in the classified propagation categories (i.e., hippocampus→EC-PC, EC→hippocampus, and only hippocampus). (*p < 0.05, ***p < 0.001, ANOVA, n = 48 slices from 6 mice of SD and ENR each). o) Quantification of detected CATs duration for the three classified propagation categories shown in m & n. (*p < 0.05, ***p < 0.001, ****p < 0.0001, ANOVA, n = 48 slices from 6 mice of SD and ENR each).
¶ 3.4.Neural coding in the spike-phase dynamics
The hippocampus uses temporal coding by theta rhythm phase precession to coordinate behavior and cognition (Harris et al., 2Oo2; Huxter et al.,2OO8). To study whether ENR would enhance the encoding conveyed by the LFP phase at the time of spiking activity,we quantified the relationship between the LFP and multi-unit spiking activity using the “phase-of-firing"coding paradigm (Montemurro et al., 2008).
A first analysis of the LFP spectrum revealed the highest power in the oscillatory theta band Supplementary Fig. 3a), so we considered theta oscillation a reliable frequency range to encode information at all firing electrodes in the network.We then quantified the LFP phases by assigning them to four color-labeled quadrants of equal duration (Fig.4a and b).We employed the phase-of-firing coding to identify those LFP phase quadrants during which spikes were discharged over long periods (Fig.4e and f).This allowed us to identify supposedly specific information contents encoded in the spatiotemporal patterned activity as opposed to the less specific spike count code shown in Fig.4c and d. Indeed,our results suggested richer information content in the spike rate associated with the LFP phase than observed in the spike counts alone (Fig. and h).The information encoded in the LFP phases of all four quadrants was significantly greater in the ENR network than in SD (Fig.4i) and strongly depended on the LFP frequency range (theta).
We further substantiated these findings by quantifying that spike counts alone conveyed bits/s of information in ENR networks compared to bits/s in SD (Fig. 4j and k). The LFP phase carried bits/s in SD, but bits/sec in the ENR network,indicating an over-proportional gain in phasedependent encoding in ENR compared to SD (Fig.4j and k).The phase of oscillatory activity conveyed in ENR vs. in SD of additional information not obtained from spike counts.Although spike counts encoded more information in ENR than in SD,the theta LFP phases carried much higher information than obtained from spike count code alone.With increasing frequencies,the extra information encoded in the LFP phases declined to reach the spike count information at frequencies greater than in SD and in ENR.Thus,information carried by LFP phases of ENR and SD networks at higher frequency bands (13-30 Hz and )waslower than but still carried more information than spike counts (Supplementary Fig. 3b and c).
In summary,these findings demonstrated the capability of our biosensor in capturing the impact of enriched experience on enhancing the density of encoded information by adding higher-dimensional complementary layers of information.Such phase-coding has been established as a mechanism for spatial representations (Harris et al., 2002),where theta oscillations provide a pacemaker for the spike trains that organize spatial information (Huxter et al., 2Oo8). Thus,our platform illustrated the impact of the prior experience in improving the characteristics of rhythmic dynamics,suggesting a mechanistic role for higher information processing during the offline state (i.e.,ex vivo brain slice conditions) of animal behavior (Sanchez-Vives and McCormick, 2000).
¶ 3.5.Experience-dependent enhancement on network-wide functional connectivity and topologically complex organization
Next, taking advantage of the rich information ingrained in our unique multi-site recordings from SD and ENR conditions, we aimed to quantify the reciprocal relationships between hippocampal-cortical subnetworks using simultaneously recorded firing patterns of concomitantly active neuronal ensembles. This was achieved by computing the cross-covariance of pairwise firing electrodes via the Pearson’s correlation coefficient (PCC) (Hu et al., 2022). Analysis of the slow oscillatory component of local field potentials (LFPs) up to 100 Hz yielded association matrices of firing coefficients, with dimensions equal to the number of firing electrodes in the 64×64 chip array (Fig. 5a, b). We found a significant enhancement in the local and global strength of spatial interactions in ENR networks compared to SD, as shown in the cross-correlogram and quantified differences between connectivity matrices (Fig. 5c–e). Both SD and ENR networks displayed a modular functional organization, featuring groups of nodes in dense clusters (white rectangles in Fig. 5c, d). Compared to SD, modules of the ENR network were more hierarchical, as indicated by large modules consisting of smaller sub-modules (white dotted rectangles in Fig. 5c, d).
To estimate mesoscale connectivity and measure the direction of information flow within correlated links, we employed multivariate Granger causality and the directed transfer function (DTF) (Hu et al., 2022). The ENR network exhibited both more unidirectional (i.e., DG → CA3, DG → CA1, DG → EC, DG → PC) and bidirectional (i.e., CA3 ↔ CA3, CA1 ↔ CA1, DG ↔ DG, Hilus ↔ Hilus, EC ↔ EC, PC ↔ PC) interaction links compared to the SD network (Fig. 5f–h and Supplementary Movies 3–4).
To assess the impact of ENR on the spatial and topological complexity of the network, we used graph-theoretic analysis to construct wiring diagrams of local and global neural activity patterns, enabling the description and quantification of the network’s organizational and communication properties (Fig. 6a). Mathematically, the network is defined as neural nodes connected by functional edges. We computed graph metrics from connectivity patterns of co-firing neuronal ensembles (corresponding to the firing electrodes of the array) encoded in the LFPs under SD and ENR conditions (Fig. 6b, c).
The degree analysis of the nodes and their incoming and outgoing connections revealed massively enhanced network complexity in ENR compared to SD (Fig. 6d and Supplementary Fig. 4).We also found a significant increase in the total number of links and degree centrality (Fig. 6e and f).According to their clustering coefficient (CC) and transitivity,ENR networks were consistently more segregated than SD networks (Rubinov and Sporns, 2O1O) (Fig. 6g and h). We also found significantly shorter paths in ENR,indicating a greater network integration (Rubinov and Sporns, 201O) (Fig. 6i).
ENR networks had more densely-interconnected nodes (hubs) and more‘rich clubs’than SD, suggesting a greater higher-order functional specialization,more network resilience,and an expansion from local to more global effects (McAuley et al., 2O07) in ENR (Fig. 6j and k).
Dimensionality of a network describes the size of its neuronal population in relation to the dynamic range of firing activity of its individual neurons.High-dimensional coding endows neural circuits with a larger coding space to facilitate the separation of overlapping activity representations (Litwin-Kumar et al., 2017; Cunningham and Yu, 2014). We found that as a function of the average connectivity,the ENR network exhibited higher dimensionality than the SD network and that in ENR with increasing connectivity (i.e.,pairwise correlation of activity patterns),dimensionality of the coding space decreased more protractedly than in SD; thus providing the network with a greater capacity for linear separability of overlapping patterns (Cayco-Gajic and Silver,2019) (Fig. 6l and Supplementary Fig. 5).
Small-word topology is a key feature of many biological networks (Watts and Strogatz,1998) that is characterized by a scale-free architecture with highly connected hub nodes and a degree distribution that decays with a power-law tail (Barabasi and Albert, 1999). Scale-free networks provide error tolerance and resilience to random failures (Albert et al.,2ooO).We found that the functional node degree distributions of SD and ENR networks indeed followed a power-law function (Fig.6m),a finding that we have previously also postulated for a transcriptomic network of adult hippocampal neurogenesis (Overall and Kempermann, 2O18).The ENR network, however, displayed a heavier tail with a more significant number of densely linked hubs compared to the SD network,which becomes visible in the log-log plots in the insets of Fig. 6m.
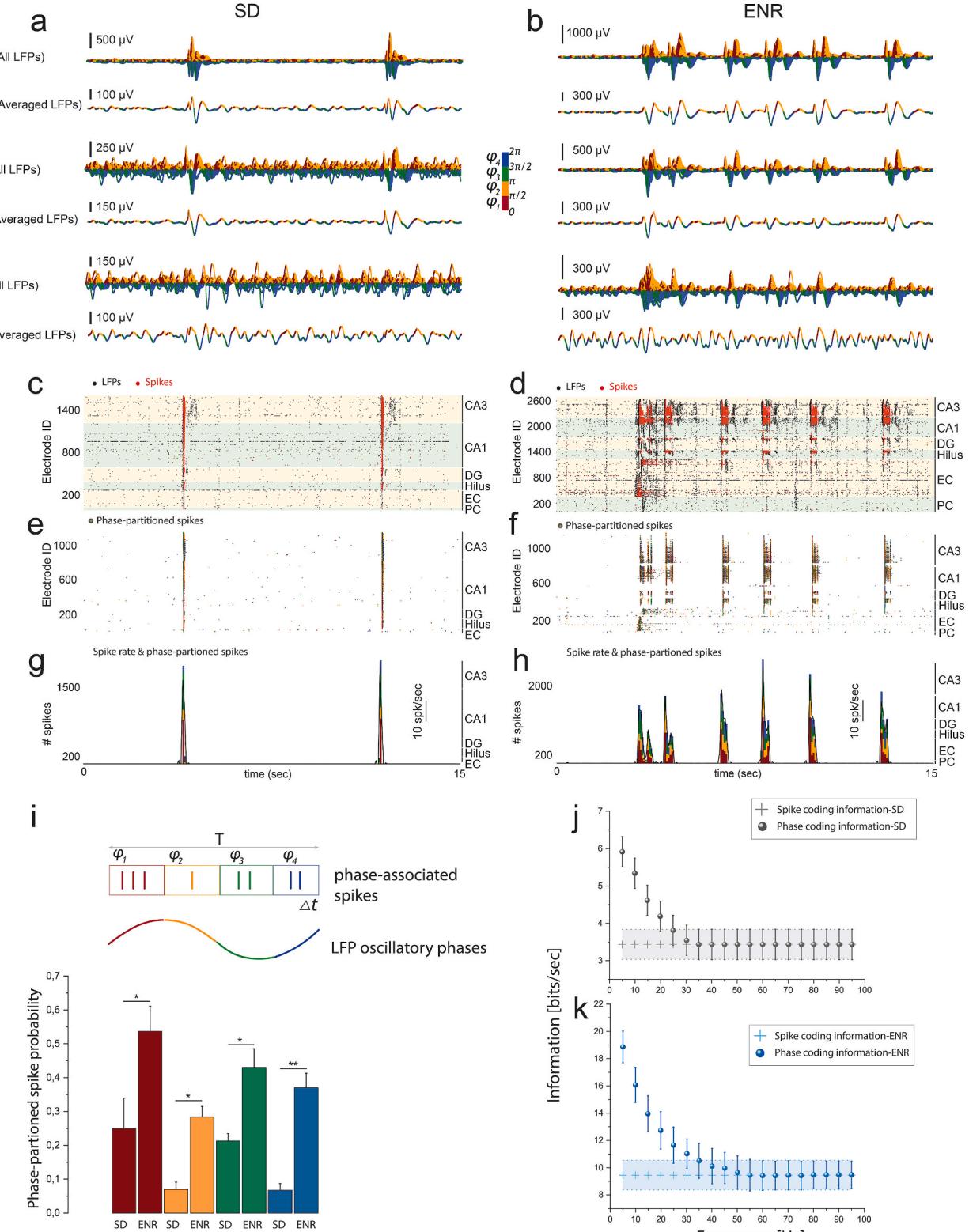
Fig. 4. Information Encoded in the Phase-of-LFP Oscillation. a-b) For SD and ENR networks, waveform traces of LFP activity from large-scale recordings of hippocampal-cortical layers (CA3, DG, and EC) showing all extracted and averaged waveforms in the theta oscillatory range (4–12 Hz) that are color-coded with four quadrants indicating the associated phase of the LFP firing. c-d) Raster plots of SD and ENR networks showing LFP and multi-unit spiking activity in all interconnected hippocampal-cortical subnetworks. Black dots for LFPs and red dots indicate spikes. e-f) The same time course in c and d but only for spikes color-coded by the phase of LFPs at which the spikes were emitted. g-h) Multi-unit spike rate in SD and ENR networks (black lines) and the amount of spikes is computed according to the LFP phase (color-coded), which indicates the same spike rate (SD vs. ENR) encodes additional information associated with the LFP phase. i) For a given time course of spike trains, the multi-unit spiking activity can be partitioned based on the slow oscillatory LFP signal into four color-coded phase quadrants. Thus, the spiking probability in the LFP phases is computed for SD and ENR networks. Compared to SD, the ENR network shows significantly higher information encoded in all quadrants of the firing phases. (*p < 0.05, **p < 0.01, ANOVA). j-k) Rate coding vs. phase coding to compare the conveyed information of hippocampal-cortical firing information in SD (j) and ENR (k). Plus sign shows the spike rate information in SD and ENR networks in j-k. (spike information, p < 10− 9, phase information, p < 10− 8, Mann-Whitney test, ANOVA).
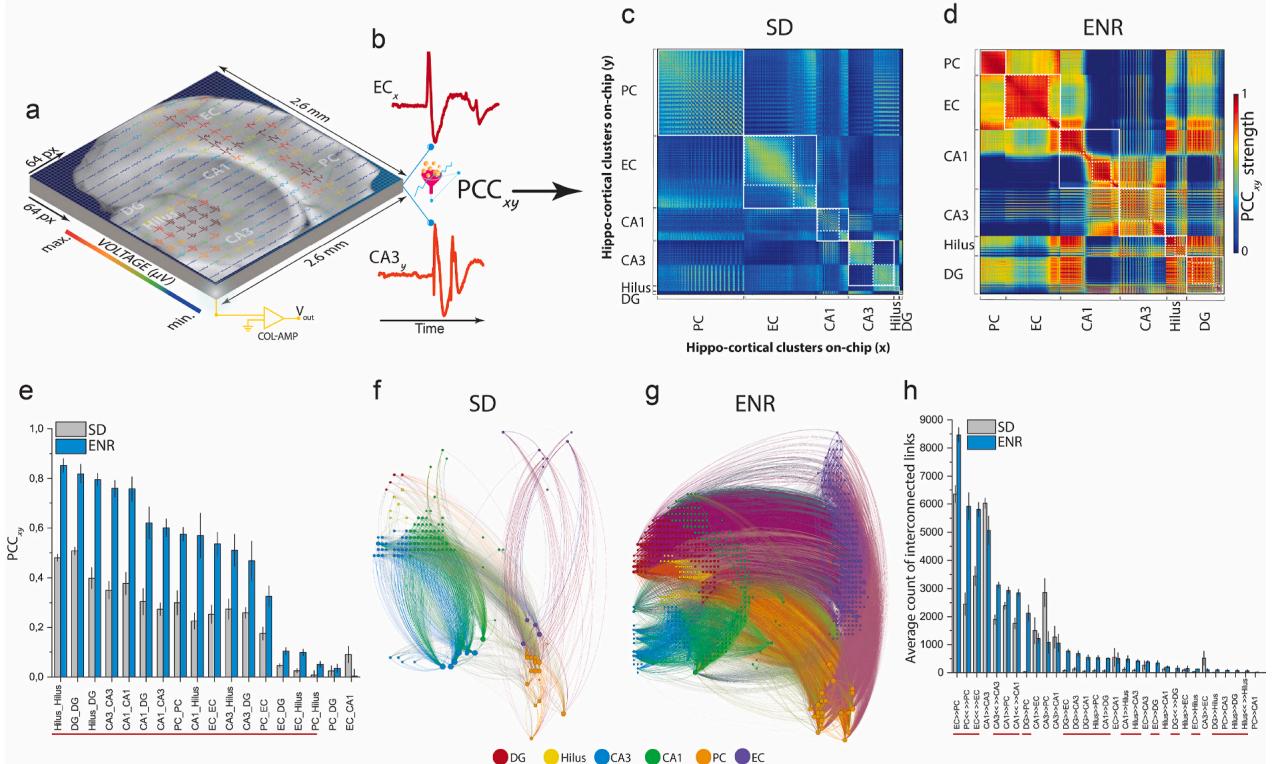
Fig. 5. Circuit-wide Functional Connectome. a) The entire Hippocampal-cortical slice is overlaid on the 64x64 microelectrode array allowing for monitoring the six interconnected subregions simultaneously with their concurrent structural information. b) Exemplary pairwise firing electrodes in the chip array to extract time courses to compute the PCC. c-d) Functional connectivity matrices representing cross-correlation of SD and ENR networks constructed and clustered by the pairs of firing neurons in their associated interconnected subnetworks. ENR displays higher correlation values in all hippocampal-cortical networks. White squares located along the diagonal illustrate modular graphs, where a set of nodes are highly connected in a region, while white dotted squares illustrate hierarchical modular graphs that are submodules of the large modules. e) Quantification of the correlation matrices shows a significant increase of PCC in interconnected regions of the ENR network compared to SD. Red-line indicates the interconnected subnetworks with significance differences (*p < 0.05, **p < 0.01 ANOVA) (n = 48 slices from 6 mice of SD and ENR each). f-g) Connectome mapping of the hippocampal-cortical network in ENR and SD. The network visualization was done using the Gephi program to illustrate 2% of the total connection in SD (node = 136, and links = 1762) and ENR (node = 661, and links = 21,648) networks, which indicates a salient higher density of connection in ENR (g) compared to SD network (f). Graph nodes are scaled according to degree strength and colored according to hippocampal-cortical module association and indicated in colored circles legends. Colored links identify the intra- and inter-cluster connections. h) Quantification of the directed interconnected links shows higher unidirectional and bidirectional communication in the ENR compared to the SD network. Red-line for significant interconnections (*p < 0.05 ANOVA) (n = 48 slices from 6 mice of SD and ENR each).
To assess the tolerance of the networks against disruptions and damage to communication between interconnected layers,we compared the connectivity robustness by quantifying the changes in the remaining links and node degree when nodes were randomly removed from the network graphs constructed based on the firing patterns in both SD and ENR (Fig.6n).In ENR,the communication strength was only slightly affected by increasing errors (i.e.,randomly removing nodes up to the maximum size of the SD network),as indicated by the relatively stable node degree and remaining links compared to SD (Fig.6n).Thus,ENR networks exhibited greater robustness against random failures than SD networks.
The failure intolerance of scale-free networks comes at the cost of increased attack vulnerability when the highly connected hubs are hit (Albert et al., 2ooO). ENR networks maintained network redundancy for a much greater number of removed nodes before reaching a total loss of communication between links (i.e., the mean lifetime decay of the degree distribution was shorter in the SD networks compared to in ENR (Supplementary Fig. 6).
In sum,prior experience yielded large-scale changes in the local and extended hippocampal-cortical circuitry,expressed in its enhanced functional connectome and increased dimensionality for encoding a larger activity space.This could facilitate efficient pattern separation to integrate different neural representations with minimum overlap (Litwin-Kumar et al., 2017; Cunningham and Yu, 2014; Alvarez et al., 2016; O’Neill et al., 2008).
¶ 4.Conclusions and outlook
We have here provided an innovative tool to address the unmet need for large-scale biosensing techniques to map experience-dependent plasticity.We applied this approach to hippocampal-cortical spatiotemporal coding that is not accessible with current fMRI imaging, electrophysiological and biosensing approaches,and computational models.We engineered a novel brain-on-chip biosensing platform to enable neurophysiological information from network-wide firing time courses and advanced computational framework to unveil rich experience impacts on activity dynamics,functional connectivity,and information dimensionality.This is the first demonstration of the ex vivo network-wide mesoscale connectome and the spatiotemporal firing pattern dynamics modulated by environmental enrichment.These findings may provide a pathway to investigate fundamental mechanisms of experience-dependent plasticity underlying high brain functions of memory,navigation,and cognition (Kempermann,2O19;Nithianantharajah and Hannan, 2Oo6). These investigations could be expanded to scrutinize the influence of dynamic environmental experiences, encompassing social interactions,physical activity,and learning processes,which play a crucial role in modulating brain function (Torquet et al., 2018; van Praag et al., 2OoO). These factors promote neural adaptations and brain network connectivity while offering potential benefits in pathological conditions such as stroke,epilepsy,dementia, stress,and aging (Nithianantharajah and Hannan, 2Oo6; Abrous et al., 2022).
Our simultaneous recordings were facilitated by optimized electrical coupling of the tissue-electrode interface,which enabled long-term stability of cellular activity with optimal spatiotemporal resolution. These measurements highlight the enhanced large-scale rhythmic dynamics in the ENR group,as evidenced by increased firing statistics and encoded information in LFPs and multi-unit activity. This enhancement may support pre-configured activity patterns necessary for spatiotemporal information processing,as well as the observed increase in gamma oscillation,synaptic and cellular properties in both in vivo and in vitro in local subnetworks in ENR-dependent behavioral conditions (Ohline and Abraham, 2019; Shinohara et al., 2013; Villette et al., 2015; Mehta et al., 2002).
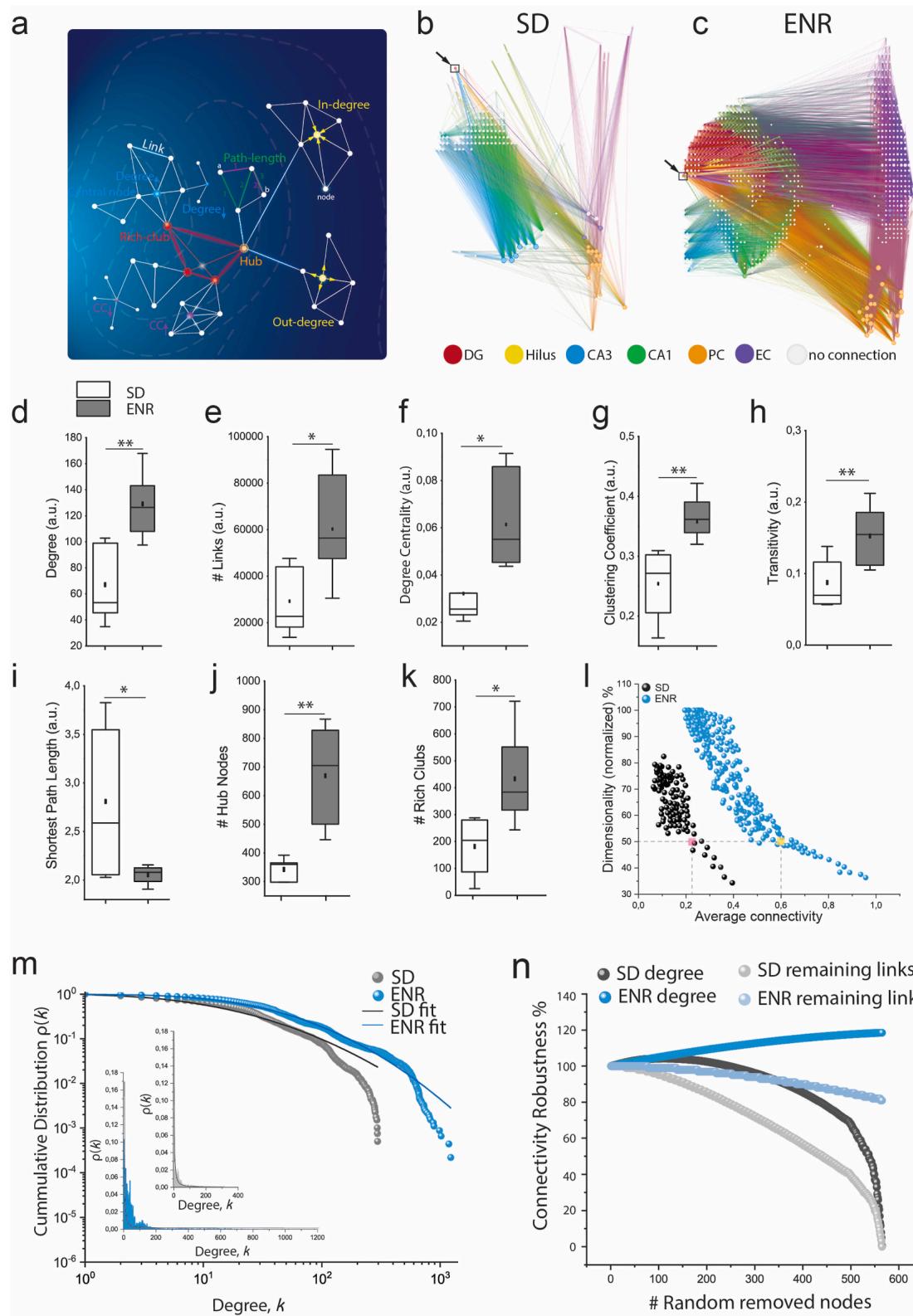
Fig. 6. Network-wide Complexity and Coding Dimensionality. a) Schematic illustration of key complex network metrics of large-scale hippocampal-cortical network on HD-chip array. b-c) Functional connectivity maps of the spatial distribution of interconnected subnetworks showing increased complexity of ENR compared to SD networks. Arrows indicate the exemplary selected nodes in the DG layer of SD and ENR to identify the associated local and global interactions. d) ENR network exhibits higher complexity shown by higher node degree (**p < 0.01 ANOVA). e-f) ENR network is significantly more densely interconnected than SD, indicated by higher numbers of links and node degree centrality (*p < 0.05 ANOVA). g-h) Graph clustering coefficient and transitivity confer significant network functional segregation in ENR than SD (**p < 0.01 ANOVA). i) ENR networks show a lower path length indicating higher functional integration than SD networks (*p < 0.05 ANOVA). j-k) ENR networks display highly dense connected hub nodes and emerging rich club organization than SD networks (**p < 0.01, *p < 0.05 ANOVA). l) ENR network exhibits a greater dimensional subspace for information coding than SD computed as a function of average connectivity (p < 10− 8 Kolmogorov-Smirnov test). Although dimensionality is reduced to 50% (colored squares), ENR maintains higher connectivity than SD. m) Scale-free functional network topology with small-world properties in SD and ENR networks indicated by the power-law distribution. The log-log plot of the cumulative connection distribution for ENR networks exhibits a significantly heavier tail than SD networks indicating low-degree nodes coexist with a few densely connected hubs, yet higher than SD networks (inset), which reach a cut-off on the power-law lead to steep decay of the tail of connectivity distribution (*p < 0.05 Kolmogorov-Smirnov test). The lognormal function fitted the power-law distribution with goodness-of-fit in a log-log plot (with a coefficient of determination R2 = 0.96 and 0.99 for SD and ENR, respectively). n) ENR networks display higher connectivity robustness to random failures quantified by the percentage of degree and remaining links after random node removal (SD vs. ENR degree and remaining links, p < 10− 8 Kolmogorov-Smirnov test).
We further characterized the large-scale initiation, propagation, and complex transmission termination of firing activity that emerged from neuronal ensembles.We determined the probability of field potential activity occurrence and its spatiotemporal topographic propagation. Afterreconstructing the CATs,we employed an unsupervised machinelearning algorithm for further analysis and classification.These classifications outlined the impact of rich experience on promoting faster information transfer and processing and enhanced large-scale spatiotemporal activity dynamics.Remarkably,this opens up new possibilities forunraveling strategies of neural information processing (Kumar et al., 2010).Nevertheless,an in-depth investigation is necessary to accurately identify the propagation mechanisms that facilitate improved information flow and network-wide pattern dynamics in ENR.This may encompass the combined roles of synaptic and non-synaptic interactions, including gap junction and ephaptic propagation (Draguhn et al.,1998; Frohlich and McCormick, 2010).
Our unique network-wide electrophysiology data and rigorous algorithms from network science (i.e.,graph and dynamical system theories) allowed us to show that ENR enhanced local functional connections to optimize network-wide rewiring,adaptability of functional remodeling and firing pattern evolvability by preserving the functional integrity of the subregional networks (Bassett et al., 2010). The enhanced connectome in ENR subnetworks displayed densely linked hub nodes characterized by a scale-free small-world topology that revealed high-dimensional coding for faster processing of the propagating neural activity,which could facilitate effcient pattern separation byproviding larger activity space (i.e.,decreased noise and variability) to embed different representations with minimum overlap (Lodge and Bischofberger, 2019).
Altogether,our study suggests a new biosensing tool for examining network-wide activity-dependent dynamics of neuronal assemblies, focusing on the enhancement attributed to the response of networks influenced by environmental enrichment. The present study is not explicitly designed to investigate the causal relation of experienceinduced network dynamics to underlying processes such as neurogenesis,which remains to be established.
This approach could elucidate the computational benefits of an ENRenhanced connectome for improved learning and memory,including flexible reversal learning,spatial remapping,and others (Mehta et al., 2002; Cuneo et al., 2Ol2). Several studies have demonstrated ENR effects on delaying the onset of neurodegenerative diseases and various types of brain injuries (Nithianantharajah and Hannan, 2Oo6).Thus, mapping and understanding large-scale experience-dependent connectome might contribute to uncovering the network deficit mechanisms underlying brain dysfunctions and identifying novel targets for the future development of more efficacious therapeutics.Given such demands and opportunities,our platform could lay the foundation for developing prosthetic devices to restore and enhance declining memory functions in aging or disease (Hampson et al., 2O18). Based on the exceptional insights into large-scale computational neural dynamics,we posit that our platform has the potential to provide a source of brain inspiration for novel neuromorphic computing solutions,enhance currentartificial intelligence methods and expand them into new applications,and mayrender radically different neural learning algorithms with unique computational intelligence (Schuman et al., 2O22; Zhang et al., 202O; Kudithipudi et al., 2022). These advancements are consistent with developments in the fields of biosensors and neuroengineering, in which neurological and mental health issues are addressed from the perspective of impaired computation in brain microcircuits.
¶ CRediT authorship contribution statement
Brett Addison Emery:Performed part of experiments and,Formal analysis,Allauthors revised,reviewed,and approved the final version of the manuscript.Xin Hu: Wrote the code for analysis and, Formal analysis.Shahrukh Khanzada: Performed part of experiments and, Formal analysis. Gerd Kempermann: Conceptualization, project, designed and performed animal experiments,supported interpretation of results, provided co-funding,co-wrote the manuscript. Hayder Amin: Conceptualization,planned,and managed the project,designed and performed experiments,developed analytical tools,Formal analysis,and co-wrote the manuscript.
¶ Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
¶ Data availability
The data supporting our findings are available within the article and its supplementary information files.The code can be shared on GitHub once the paper has been conditionally accepted.
¶ Acknowledgment
This study was financed from basic institutional funds (DZNE).We would also like to acknowledge the platform for behavioral animal testing at the DZNE-Dresden (Alexander Garthe,Anne Karasinsky, Sandra Ginther,and Jens Bergmann) for their support.We would like to acknowledge that a portion of Fig.la was created using the platform BioRender.com.
¶ Appendix A. Supplementary data
Supplementary data to this article can be found online at https://doi. org/10.1016/j.bi0s.2023.115471.
¶ References
Abbott, J.,et al., 2O2o. A nanoelectrode array for obtaining intracellular recordings from thousands of connected neurons. Nat. Biomed. Eng. 4, 232-241.
Abrous, D.N., Koehl, M., Lemoine, M.,2022. A Baldwin interpretation of adult hippocampal neurogenesis: from functional relevance to physiopathology. Mol. Psychiatr. 27, 383-402.
Aimone, J.B., Gage, F.H., 2011. Modeling new neuron function: a history of using computational neuroscience to study adult neurogenesis. Eur. J. Neurosci. 33, 1160-1169.
Aimone,J.B.,Wles,J,Gage,F.H,.Computatioaliuenceofadutnerogis on memory encoding. Neuron 61,187-202.
Albert,R., Jeong, H., Barabasi, A.L., 20oo. Error and attack tolerance of complex networks. Nature 406, 378-382.
Altman, J., Das, G.D.,1965. Autoradiographic and histological evidence of postnatal hippocampal neurogenesis in rats. J. Comp. Neurol. 124, 319-335.
Alvarez, D.D., et al., 2016. A Disynaptic Feedback Network Activated by Experience Promotes the Integration of New Granule Cels, vol. 354, pp. 459-466.
Amaral, D.G., Witter, M.P.,1989. The three-dimensional organization of the hippocampal formation: a review of anatomical data. Neuroscience 31, 571-591.
Amin,H., Nieus, T., Lonardoni, D., Maccione, A., Berdondini, L., 2017. High-resolution bioelectrical imaging of Aβ-induced network dysfunction on CMOS-MEAs for neurotoxicity and rescue studies. Sci. Rep. 7, 2460.
Amin,H., et al., 20l6. Electrical responses and spontaneous activity of human iPsderived neuronal networks characterized for 3-month culture with 4096-electrode arrays. Front. Neurosci. 10, 1-15.
Amin,H.,Dipalo,M., De Angelis,F.,Berdondini,L.,2018.Biofunctionalized 3D nanopillar arrays fostering cell-guidance and promoting synapse stability and neuronal activity in networks.ACS Appl. Mater.Interfaces 1-9. htps://doi.org/ 10.1021/acsami.8b00387.
Andersen, Per,Morris, Richard, Amaral, David, Bliss, Tim, O’Keefe, J. (Eds.),2007. The hippocampus Book. - PsycNET… Oxford University Press.
Angotzi, G.N., et al., 2019. SiNAPS: an implantable active pixel sensor CMOS-probe for simultaneous large-scale neural recordings. Biosens. Bioelectron. 126, 355-364.
Barabasi, A.-L., Albert, R., 1999. Emergence of scaling in random networks. Science 286, 509-512.
Bassett, D.S., et al., 2010. Efficient physical embedding of topologically complex information processing networks in brains and computer circuits. PLoS Comput. Biol. 6.
Berdondini,L. et al.,20o5. High-density electrode arry for imaging in vitro electrophysiological activity. Biosens. Bioelectron. 21,167-174
Bergami, M., etal., 2015.Acritical period for experience-dependent remodeling of adultborn neuron connectivity. Neuron 85, 710-717.
Bird, C.M., Burgess, N., 20o8. The hippocampus and memory: insights from spatial processing. Nat. Rev. Neurosci. 9, 182-194.
Butler,J.L,usenO5.Hpoamanerkosilos-etisihtsfr in vitro experiments. Curr. Opin. Neurobiol. 31, 40-44.
Buzsaki, G., 1989. Two-stage model of memory trace formation: a role for ‘noisy’ brain states. Neuroscience 31, 551-570.
Buzsaki, G., 2002. Theta oscillations in the Hippocampus. Neuron 33, 1-16.
Buzsaki, G., Mizuseki, K.,2014. The log-dynamic brain: how skewed distributions affect network operations. Nat. Rev. Neurosci.15, 264-278.
Buzsaki, G., etal.,2015. Tools for probing local circuits: high-density silicon probes combined with optogenetics. Neuron 86, 92-105.
Cayco-Gajic,N.A.,Silver,R.A.,2019. Re-Evaluating circuit mechanisms underlying pattern separation. Neuron 101, 584-602.
Christian, K.M., Song, H., Ming, G.L.,2014. Functions and dysfunctions of adult hippocampal neurogenesis. Annu. Rev. Neurosci. 37, 243-262.
Colgin,L.L., et al., 2oo9. Frequency of gamma oscillations routes flow of information in the hippocampus. Nature 462, 353-357.
Cuneo,J.I., Quiroz, N.H., Weisz, V.I., Argibay,P.F., 20l2. The computational influence of neurogenesis in the processing of spatial information in the dentate gyrus. Sci. Rep. 2.
Cunningham, J.P., Yu, B.M., 2014. Dimensionality reduction for large-scale neural recordings. Nat. Neurosci. 1711 (17),1500-1509, 2014.
Draguhn, A., Traub, R.D., Schmitz, D., Jeferys, J.G.R.,1998. Electrical coupling underlies high-frequency oscillations in the hippocampus in vitro. Nature 394, 189-192.
Emery,B.A.,et al.,2022.Large-scale multimodal neural recordings on a high-density neurochip :olfactory bulb and hippocampal networks.Ieee Embs 42-45.https://doi. org/10.1109/EMBC48229.2022.9871961.
Ferrea, E., et al.,2012. Large-scale, high-resolution electrophysiological imaging of field potentials in brain slices with microelectronic multielectrode arrays. Front. Neural Circ. 6, 1-14.
Francis, J.T., Gluckman, B.J., Schi, S.J., 20o3. Sensitivity of neurons to weak electric fields. J. Neurosci. 23, 7255-7261.
Frenkel, C. 2021. Sparsity provides a competitive advantage. Nat. Mach. Intell. 3, 742-743.
Frohlich,F., McCormick, D.A.,20lo.Endogenous electric fields may guide neocortical network activity. Neuron 67, 129-143.
Garthe, A., Roeder,I., Kempermann, G., 2016. Mice in an enriched environment learn more flexibly because of adult hippocampal neurogenesis. Hippocampus 26, 261-271.
Hagberg, A.A., Schult, D.A., Swart, P.J., 20o8. Exploring network structure, dynamics, and functionusing NetworkX. In: Varoquaux, G., Vaught, Travis (Eds.), 7th Python in Science Conference (SciPy 2008), pp.11-15.
Hampson, R.E., et al., 2018. Developing a hippocampal neural prosthetic to facilitate human memory encoding and recall. J. Neural. Eng. 15, aaaed7.
Harris, K.D., et al., 2Oo2. Spike train dynamics predicts theta-related phase precession in hippocampal pyramidal cels. Nature 417, 738-741.
Holtmaat, A., Svoboda, K., 2o9.Experience-dependent structural synaptic plasticityin the mammalian brain. Nat. Rev. Neurosci. io, 647-658.
Hu, X., Khanzada, S., Klitsch, D., Calegari, F., Amin, H., 2022. Implementation of biohybrid olfactory bulb on a high-density CMOS-chip to reveal large-scale spatiotemporal circuit information. Biosens. Bioelectron.198,113834.
Huang, Y., Wiiams, J.C., Johnson, S.M., 2012. Brain slice ona chip: opportunities and challenges of applying microfluidic technology to intact tissues. Lab Chip 12, 2103-2117.
Hurley, N., Rickard, S., 2Oo9. Comparing measures of sparsity. IEEE Trans. Inf. Theor. 55, 4723-4741.
Huxter,J.R.,Senior,T.J.Allen,K., Csicsvari, J.,2o08.Theta phase-specificcodes for two-dimensional position, trajectory and heading in the hippocampus. Nat. Neurosci. 11, 587-594.
Imfeld, K., etal., 2oo8.Large-scale, high-resolution data acquisition system for extracellular recording of electrophysiological activity.IEEE Trans. Biomed.Eng.55, 2064-2073.
Jercog, D., et al., 2017. UP-DOWN cortical dynamics reflect state transitions in a bistable network. Elife 6, 1-33.
Jun, J.J., etal., 2O17. Fully integrated silicon probes for high-density recording of neural activity. Nature 551, 232-236.
Kay, K.,et al., 2016.A hippocampal network for spatial coding during immobility and sleep. Nature 531,185-190.
Kempermann, G. 2Oo3. Why new neurons? possible functions for adult hippocampal neurogenesis. J. Neurosci. 23, 635-638.
Kempermann, G., 2019. Environmental enrichment, new neurons and the neurobiology of individuality. Nat. Rev. Neurosci. 20, 235-245.
Kempermann, G.,Song,H., Gage,F.H.,2015. Neurogenesis in the Adult hippocampus, pp. 243-250. https://doi.org/10.1101/cshperspect.a018812.
Kim,D.J.,Min,B.K., 2020. Rich-club inthe bain’s macrostructure: insights from graph theoretical analysis. Comput. Struct. Biotechnol. J. 18, 1761-1773.
Kudithipudi, D.,etal., 2022. Biological underpinnings for lifelong learning machines. Nat. Mach. Intell. 4, 196-210.
Kumar,A., Rotter, S.,Aertsen, A.,2010. Spiking activity propagation in neuronal networks: reconciling different perspectives on neural coding. Nat. Rev. Neurosci. 11, 615-627.
Lepousez, G., Valley, M.T., Lledo, P.-M., 2013. The impact of adult neurogenesis on olfactory bulb circuits and computations. Annu. Rev. Physiol. 75, 339-363.
Lisman, J.E.,999.Relating hppocampal circuitrytounction: recallof sequences by reciprocal dentate-CA3 interactions. Neuron 22, 233-242.
Lisman,J.E.,TlaminiLM,Rafone,A.,25.Recallofmemoryqeces by interaction of the dentate and CA3: a revised model of the phase precession. Neural Network. 18, 1191-1201.
Lisman, J.,etal., 20l7. Viewpoints: how the hippocampus contributes to memory, navigation and cognition. Nat. Neurosci. 20, 1434-1447.
Litle,D.M., Foxely, S., Lazarove, O., 2012. A preliminary study targeting neuronal pathways activated following environmental enrichment by resting state functional magnetic resonance imaging. J. Alzheimers. Dis. 32, 101-107.
Litwin-Kumar,A., Harris, K.D., Axel, R., Sompolinsky, H., Abbot, L.F., 2017. Optimal degrees of synaptic connectivity. Neuron 93, 1153-1164.e7.
Lodge,M., Bischofberger, J.,2019.Synaptic properties of newly generated granule cels support sparse coding in the adult hippocampus. Behav. Brain Res. 372, 112036.
Maccione,A., et al., 2Oo9. A novel algorithm for precise identification of spikes in extracellularly recorded neuronal signals. J. Neurosci. Methods 177, 241-249.
Manno, F.A.M., et al., 2022. Environmental enrichment leads to behavioral circadian shifts enhancing brain-wide functional connectivity between sensory cortices and eliciting increased hippocampal spiking. Neuroimage 252.
Mazzoni, A., Logothetis,N.K.,Panzeri, S.,2o13.Information content of local field potentials: experiments and models.Princ.Neural Coding 411-430. https://doi.org/ 10.1201/b14756.
McAuley, J.J., DaFontoura Costa,L., Caetano,T.S., 2007. Rich-club phenomenonacross complex network hierarchies. Appl. Phys. Lett. 91, 2-5.
McCormick, D.A., Contreras, D., 20o1. On the celular and network bases of epileptic seizures. Annu. Rev. Physiol. 63, 815-846.
Mehta,M.R.,Lee, A.K., Wilson, M.A, 2002. Role of experienceand oscilations in transforming a rate code into a temporal code. Nature 417, 741-746.
Miler, S.M., Sahay, A.,2019. Functions of adult-bo neurons inhippocampal memory interference and indexing. Nat. Neurosci. 22, 1565-1575.
Mohammed,A.H.,etal.,20o2.Environmental enrichmentandthebrain.Prog.Brain Res. 138,109-133.
Montemurro, M.A., Rasch, M.J., Murayama, Y., Logothetis, N.K., Panzeri, S., 2008. Phase-of-Firing coding of natural visual stimuli inprimary visualcortex. Curr. Biol. 18,375-380.
Myers,C.E.,Scharfman,H.E.,2011.Pattern separationin the dentate gyrus: arole for the CA3 backprojection. Hippocampus 21, 1190-1215.
Nithianantharajah, J., Hannan, A.J., 2oo6. Enriched environments, experiencedependent plasticity and disorders of the nervous system. Nat. Rev. Neurosci. 7, 697-709.
Ohline, S.M., Abraham, W.C., 2019. Environmental enrichment effects on synaptic and cellular physiology of hippocampal neurons. Neuropharmacology 145, 3-12.
Overall, R.W., Kempermann, G., 2018. The small world of adult hippocampal neurogenesis. Front. Neurosci. 12, 1-12.
O’Neill, J., Senior, T.J.,Allen, K., Huxter, J.R., Csicsvari, J., 2oo8. Reactivation of experience-dependent cell assembly patterns in the hippocampus. Nat. Neurosci.11, 209-215.
Panas, D., et al., 2o15. Sloppiness in spontaneously active neuronal networks. J. Neurosci. 35, 8480-8492.
Restivo,L., Niibori, Y., Mercaldo, V., Josselyn, S.A., Frankland,P.W., 2015. Development of adult-generated cell connectivity with excitatory and inhibitory cell populations in the hippocampus. J. Neurosci. 35, 10600-10612.
Reyes, A.D., 2019. Neuronal signals thoroughly recorded. Nature 575, 38-39.
Rubinov,M., Sporns, O., 201o. Complex network measures of brain connectivity: uses and interpretations. Neuroimage 52, 1059-1069.
Sanchez-Vives,M.V., McCormick, D.A., 20oo. Cellular and network mechanisms of rhytmic recurrent activity in neocortex. Nat. Neurosci. 3, 1027-1034.
Scharfman, H.E., 2oo7. The CA3‘backprojection’ to the dentate gyrus. Prog. Brain Res. 163, 627-637.
Schroeter, M.S., Charlesworth, P., Kitzbichler,M.G., Paulsen, O., Bullmore, E.T., 2015. Emergence of rich-club topology and coordinated dynamics in development of hippocampal functional networks in vitro. J. Neurosci. 35, 5459-5470.
Schuman, C.D., et al., 2022. Opportunities for neuromorphic computing algorithms and applications. Nat. Comput. Sci. 2, 10-19.
Shinohara, Y., Hosoya, A., Hirase, H., 2O13. Experience enhances gamma oscillations and interhemispheric asymmetry in the hippocampus. Nat. Commun. 4.
Sirota, A., Buzsaki, G., 2oo5. Interaction between neocortical and hippocampal networks via slow oscillations. Thalamus Relat. Syst.3, 245-259.
Soe, A.K., Nahavandi, S., Khoshmanesh, K., 2O12. Neuroscience goes on a chip. Biosens. Bioelectron. 35, 1-13.
Torquet, N., et al., 2018. Social interactions impact on the dopaminergic system and drive individuality. Nat. Commun. 9, 1-11.
Tuncdemir, S.N., Lacefield, C.O., Hen, R., 2019. Contributions of adult neurogenesis to dentate gyrus network activity and computations. Behav. Brain Res. 374.
Urban-Wojcik,E.J.,etal.,2021.Diversity of daily activities is associated with greater hippocampal volume. Cognit.Affect Behav.Neurosci. https://doi.org/10.3758/ S13415-021-00942-5.
van Praag,H., Kempermann, G., Gage, F.H., 2ooo. Neural consequences of enviromental enrichment. Nat. Rev. Neurosci.1, 191-198.
Villette, V., Malvache, A., Tressard, T.,Dupuy, N., Cossart, R., 2015. Internally recurring hippocampal sequences as a population template of spatiotemporal information. Neuron 88, 357-366.
Watrous,A.J., Fell, J., Ekstrom, A.D.,Axmacher, N., 2015. More than spikes: common oscillatory mechanisms for content specific neural representations during perception and memory. Curr. Opin. Neurobiol. 31, 33-39.
Watts,D.J., Strogatz, S.H., 1998. Collective dynamics of ‘small-world’ networks.Nature 393,440-442.
Wu, Y., et al., 2022. Brain-inspired global-local learning incorporated with neuromorphic computing. Nat. Commun. 13, 1-14.
Zhang,W., et al., 2020. Neuro-inspired computing chips. Nat. Electron. 3, 371-382.